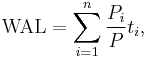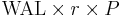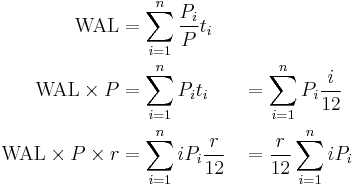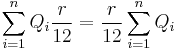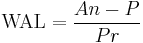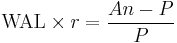Weighted-average life

In finance, the weighted-average life (WAL) of an amortizing loan or amortizing bond, also called average life,^[1]^[2]^[3] is the weighted average of the times of the principal repayments: it's the average time until a dollar of principal is repaid.

In a formula,^[4]

$\text{WAL} = \sum_{i=1}^n \frac {P_i}{P} t_i,$

where:

$P$ is the (total) principal,
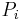$P_i$ is the principal repayment in coupon $i$ , hence
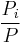$\frac{P_i}{P}$ is the fraction of the principal repaid in coupon $i$ , and
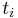$t_i$ is the time (in years) from the start to coupon $i$ .

If desired, 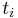$t_i$ can be expanded as 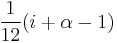$\frac{1}{12}(i%2B\alpha-1)$ for a monthly bond, where $\alpha$ is the fraction of a month between settlement date and first cash flow date.

1 Related concepts
2 Applications
3 Examples
4 Total Interest
- 4.1 Proof
- 4.2 Computing WAL from amortized payment
5 WALs of classes of loans
6 Notes and references
7 See also

Related concepts

WAL should not be confused with the following distinct concepts:

Bond duration: Bond duration is the weighted average of the times of the present values of all the cash flows (not distinguishing between principal and interest), while WAL is the weighted average of the actual amounts of the principal payments (disregarding interest, and not discounting). For an amortizing loan with equal payments, the WAL will be higher than the duration, as the early payments are weighted towards interest, while the later payments are weighted towards principal, and further, taking present value (in duration) discounts the later payments.
Time until 50% of the principal has been repaid: WAL is a mean, while "50% of the principal repaid" is a median; see difference between mean and median. This is a common misunderstanding.^[5] Since for a flat payment amortizing loan, principal outstanding is a concave function (of time), at the WAL, less than half the principal will have been paid off. Intuitively, this is because most of the principal repayment happens at the end. Formally, the distribution of repayments is negative skewed: the small principal repayments at the beginning drag down the WAL (mean) more than they reduce the median.
Weighted Average Maturity (WAM): WAM is an average across several loans, and applied to pools of mortgages, instead of an average of principal repayments for a single loan. There is also a notion of WAL within pools of loans, quite similar to but technically different from WAM, and unrelated to WAL as discussed in this article.^[6]

Applications

WAL is a measure that is useful in credit risk analysis on fixed income securities, bearing in mind that the main credit risk of a loan is the risk of loss of principal. The primary reason for this is that, all else equal, a longer-dated bond (i.e. a greater maturity) has greater risk than its shorter-dated counterpart.

WAL should not be used to calculate interest rate risk, as it only includes the principal payments, omitting interest payments. Instead, one should use bond duration, which takes the average of all cash flows.

Examples

On a 30-year loan, paying equal amounts monthly, one has the following WALs, for the given annual interest rates (and corresponding amortizing payments, calculated via an amortization calculator, using a principal of $100,000):

Rate	Payment	Total Interest	WAL Calculation	WAL
4%	$477.42	$71,871.20	$71,871.20/($100,000*4%)	17.97
8%	$733.76	$164,153.60	$164,153.60/($100,000*8%)	20.52
12%	$1,028.61	$270,299.60	$270,229.60/($100,000*12%)	22.52

Note that as interest rate increases, WAL increases. WAL is independent of principal, though payments and total interest are proportional to principal.

See below for relations between amortized payments, total interest, and WAL.

Total Interest

WAL allows one to easily compute the total interest payments, which is given by:

$\text{WAL} \times r \times P$

where r is the annual interest rate and P is the initial principal.

This can be understood intuitively as: "A dollar of principal is outstanding for on average the WAL, hence the interest on an average dollar is 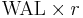$\text{WAL} \times r$ , and now one multiplies by the principal to get total interest payments".

Proof

More rigorously, one can derive the result as follows. To ease exposition, assume that payments are monthly, so periodic interest rate is annual interest rate divided by 12, and time 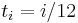$t_i = i/12$ (time in years is period number in months, over 12).

Then:

$\begin{align} \text{WAL} &= \sum_{i=1}^n \frac {P_i}{P} t_i\\ \text{WAL} \times P &= \sum_{i=1}^n P_i t_i &&= \sum_{i=1}^n P_i \frac{i}{12}\\ \text{WAL} \times P \times r &= \sum_{i=1}^n iP_i \frac{r}{12} &&= \frac{r}{12} \sum_{i=1}^n iP_i \end{align}$

Total interest is

$\sum_{i=1}^n Q_i \frac{r}{12} = \frac{r}{12}\sum_{i=1}^n Q_i$

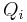where $Q_i$ is the principal outstanding at the beginning of period i (it's the principal on which the i interest payment is based). The statement reduces to showing that 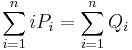$\sum_{i=1}^n iP_i=\sum_{i=1}^n Q_i$ . Both of these quantities are the time-weighted total principal of the bond (in periods), and they are simply different ways of slicing it: the 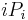$iP_i$ sum counts how long each dollar of principal is outstanding (it slices horizontally), while the 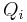$Q_i$ counts how much principal is outstanding at each point in time (it slices vertically).

Working backwards, 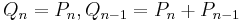$Q_n=P_n, Q_{n-1}=P_n%2BP_{n-1}$ , and so forth: the principal outstanding when k periods remain is exactly the sum of the next k principal payments. The principal paid off by the last (nth) principal payment is outstanding for all n periods, while the principal paid off by the second to last ((n − 1)th) principal payment is outstanding for n − 1 periods, and so forth. Using this, the sums can be re-arranged to be equal.

For instance, if the principal amortized as $100, $80, $50 (with paydowns of $20, $30, $50), then the sum would on the one hand be 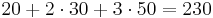$20%2B2\cdot 30 %2B 3\cdot 50=230$ , and on the other hand would be 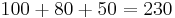$100%2B80%2B50=230$ . This is demonstrated in the following table, which shows the amortization schedule, broken up into principal repayments, where each column is a 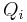$Q_i$ , and each row is $iP_i$ :

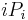230	100	80	50
1 × 20	20
2 × 30	30	30
3 × 50	50	50	50

Computing WAL from amortized payment

The above can be reversed: given the terms (principal, tenor, rate) and amortized payment A, one can compute the WAL without knowing the amortization schedule. The total payments are 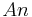$An$ and the total interest payments are 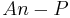$An-P$ , so the WAL is

$\text{WAL} = \frac{An-P}{Pr}$

Similarly, the total interest as percentage of principal is given by 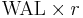$\text{WAL} \times r$ :

$\text{WAL} \times r = \frac{An-P}{P}$

WALs of classes of loans

The WAL of a bullet loan (non-amortizing) is exactly the tenor, as the principal is repaid precisely at maturity.

For a given tenor, WAL increases with increasing coupon, as the principal payments become increasingly back-loaded. For a coupon of 0%, where the principal amortizes linearly, the WAL is exactly half the tenor plus half a period, because principal is repaid in arrears (at the end of the period). So for a 30 year 0% loan, paying monthly, the WAL is 15 1/24 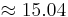$\approx 15.04$ years.

In loans that allow prepayment, the WAL cannot be computed from the amortization schedule: one must also make an assumption about the prepayment behavior, and the quoted WAL will be an estimate, which may be called simulated average life and based on an option-adjusted spread (OAS) model.^[7] This is particularly used in mortgage-backed securities.

Notes and references

^ PIMCO glossary
^ Bloomberg Glossary
^ (Fabozzi 2000, pp. 588–589)
^ (Fabozzi 2000, pp. 616–617)
^ Investopedia makes this error, as does Average Life in MSRB glossary in the context of bonds.
^ Weighted Average Life:Enhancing Money Market Fund Transparency
^ (Fabozzi 2000, pp. 805)

Fabozzi, Frank J. (2000), The handbook of fixed income securities, ISBN 0870949853